Метод расчёта линейных в установившемся режиме в отношении гармонических сигналов.
Этот метод использует обобщения понятий сопротивления, напряжения, силы тока (и прочих) до комплексных величин, являющихся функцией частоты.
Геометрическая интерпретация[]
Амплитуда и фаза[]
Гармоническую функцию можно выразить формулой:
где
- — амплитуда,
- — циклическая частота,
- — начальная фаза.
Для электрических систем функция может описывать напряжение (приведено для примера), силу тока, магнитный поток, заряд, а также в приложении к электрическим средам — проекции электрического поля, плотности тока и т. п.
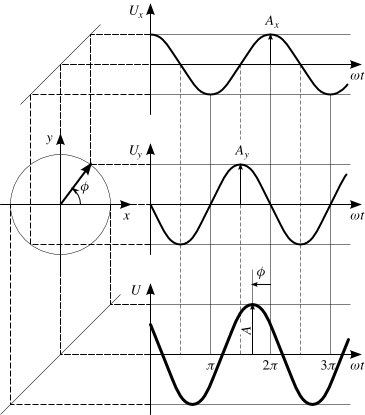
Эти два параметра можно представить в виде вектора на плоскости, где амплитуда — длина, а фаза — угол, отсчитанный по традиции от положительного направления оси абсцисс против часовой стрелки.
Изменение сигнала по времени можно представить вращением вектора вокруг начала координат против часовой стрелки с угловой скоростью ω, и тогда проекция вектора на ось x или у будет описывать гармоническую функцию:
Линейные преобразования гармонических функций[]
Любое линейное преобразование может увеличивать или уменьшать амплитуду на постоянное число раз и изменять фазу на постоянный угол, или добавлять и при том не меняет частоту. Так что возможно рассматривать поведение системы на определённой частоте, оперируя только амплитудой и фазой.
В геометрическом представлении сложение двух сигналов будет представляться в виде сложения двух векторов, усиление (или ослабление) — изменением длины, а сдвиг фазы — поворотом (изменением направления). Проекции векторов на оси координат также имеют важное значение. Гармонический сигнал с произвольной амплитудой и фазой можно представить как сумму двух сигналов — сигнала с нулевой фазой и сигнала с фазой (90°). Координаты по x и y при этом будут означать амплитуду этих компонентов.
Активное и реактивное сопротивление[]
Напряжение и ток на резисторе подчиняются закону Ома, и таким образом имеют одно значение фазы, а отношение их амплитудных значений равно сопротивлению.
Если же пропустить гармонический сигнал через конденсатор или катушку индуктивности, то амплитуды напряжения и тока также будут находиться в некотором соотношении, но разница в фазе будет составлять 90° для индуктивности и −90° для конденсатора. Это значит, что амплитуды тока и напряжения через них можно выразить в виде формулы:
где величина, называемая реактивным сопротивлением. При этом для положительного сдвига фазы принимается положительным, а для отрицательного — отрицательным, что позволяет единообразно описывать индуктивность и ёмкость (сигналы с фазами +90° и −90° находятся в противофазе, то есть находятся в отрицательном соотношении). Значение реактивного сопротивления для индуктивности и ёмкости выражается формулами:
Понятие комплексной амплитуды[]
Геометрическую интерпретацию легко перенести на интерпретацию в комплексных числах, считая амплитуду модулем комплексного числа, а фазу — аргументом. Такое число называется комплексной амплитудой, и обозначается символом циркумфлекса («крышки») над символом амплитуды.
Разложение по координатам будет соответствовать действительной и мнимой части комплексной амплитуды. Сигнал таким образом можно выразить через комплексную амплитуду следующим образом:
В такой системе сложение сигналов представимо сложением комплексных чисел.
Как изменение амплитуды сигнала, так и сдвиг фазы при этом представимы одной операцией, причём коэффициент передачи (усиления / ослабления) выражается модулем множителя, а сдвиг — его аргументом.
Расширение электротехнических законов на комплексные амплитуды[]
Закон Ома выражает соотношение напряжения (для простоты будем рассматривать закон Ома для участка цепи, в случае закона Ома для полной цепи всё аналогично до замены напряжения на ЭДС) и тока в цепи. Коэффициентом соответствия здесь служит сопротивление:
Аналогом сопротивления в методе комплексных амплитуд является импеданс (). Таким образом закон Ома будет выглядеть так:
Это позволяет единообразно описывать поведение как активного сопротивления, так и реактивного (конденсаторы, индуктивности) и производить с ними операции аналогично операциям с активным сопротивлением.